有限元分析常用接触算法及工程应用

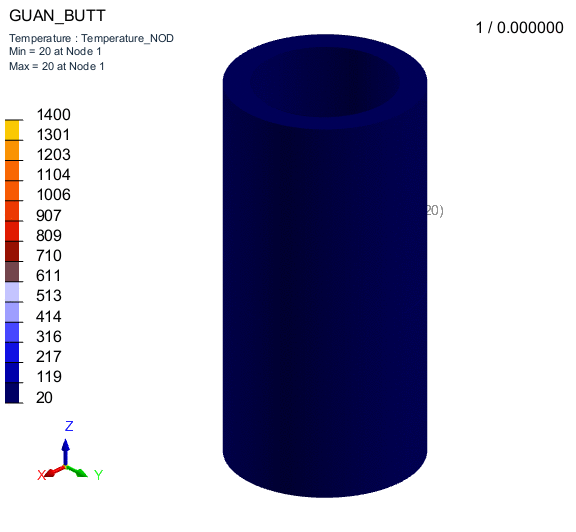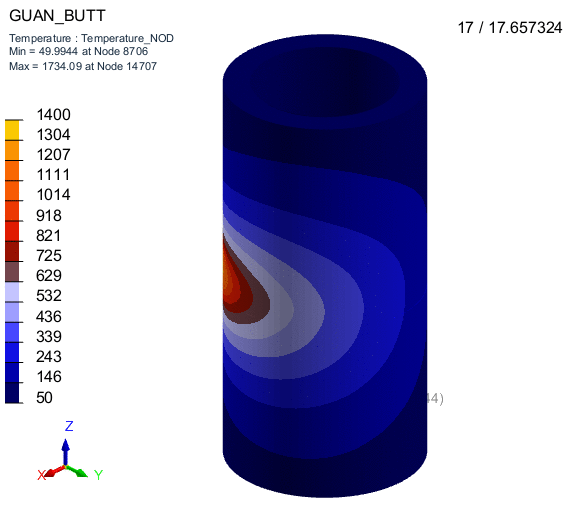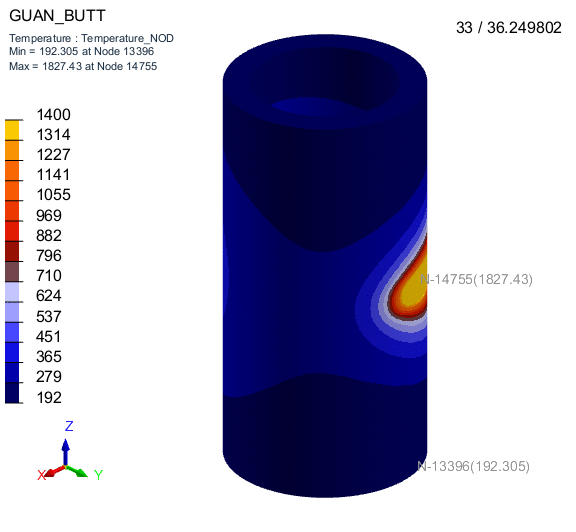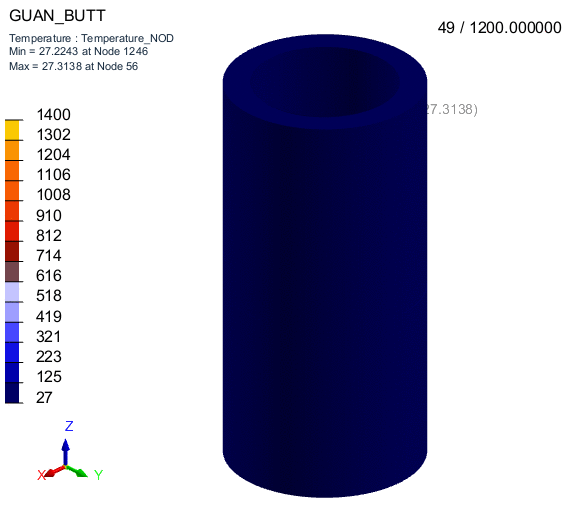
有限元分析（Finite Element Analysis，FEA）作为一种数值模拟方法，在工程领域得到了广泛应用。其中，接触问题的模拟是FEA中一个重要的研究方向。接触问题是指两个或多个物体相互接触时所产生的力学行为。在模拟接触问题时，接触算法的选择至关重要。本文将介绍几种常用的接触算法，并结合工程实例进行说明。

常见的接触算法

1. 罚函数法

  • 原理： 通过在接触面之间引入一个弹性力来模拟接触约束。当接触发生时，弹性力的大小与穿透深度成正比。
  • 优点： 实现简单，计算效率高。
  • 缺点： 罚参数的选择对结果影响较大，过大的罚参数可能导致刚度矩阵病态，过小的罚参数可能导致穿透。
  • 工程应用：
    • 模具成型： 模拟模具与工件之间的接触，预测成形过程中的应力和变形。
    • 冲压成形： 模拟冲压过程中的板料与模具之间的接触，分析板料的变形和裂纹扩展。

2. 拉格朗日乘子法

  • 原理： 引入拉格朗日乘子来严格满足接触约束条件。
  • 优点： 可以精确地满足接触约束，不受罚参数的影响。
  • 缺点： 引入了额外的未知量，增加了计算量。
  • 工程应用：
    • 焊接模拟： 模拟焊接过程中焊缝与基材之间的接触，分析焊接应力和残余应力。
    • 装配分析： 模拟零件之间的装配过程，分析接触力的大小和分布。

3. 增广拉格朗日法

  • 原理： 结合罚函数法和拉格朗日乘子法，在保证接触约束的同时，提高收敛性。
  • 优点： 结合了两种方法的优点，收敛性好，对罚参数的依赖性较小。
  • 缺点： 计算量较大。
  • 工程应用：
    • 摩擦接触： 模拟具有摩擦力的接触问题，分析摩擦力对结构的影响。
    • 冲击碰撞： 模拟物体之间的冲击碰撞，分析接触力的时间历程。

4. 基于节点的接触算法

  • 原理： 将接触面离散为节点，通过节点之间的相对运动来判断是否发生接触。
  • 优点： 实现简单，计算效率高，适用于大变形问题。
  • 缺点： 精度较低，可能出现节点穿透现象。
  • 工程应用：
    • 橡胶密封件： 模拟橡胶密封件与零件之间的接触，分析密封性能。
    • 生物力学： 模拟软组织之间的接触，分析组织的变形和应力。

总结

选择合适的接触算法取决于具体的工程问题和计算资源。对于一般的接触问题，罚函数法和增广拉格朗日法是常用的选择。对于需要精确满足接触约束的问题，拉格朗日乘子法是更好的选择。对于大变形问题，基于节点的接触算法是一种有效的选择。

需要注意的是，接触算法的选择还受到有限元软件的影响。不同的有限元软件提供了不同的接触算法和设置选项。在进行接触分析时，需要仔细阅读软件的帮助文档，选择适合的算法和参数

CAE用户分类及特点分析

CAE（Computer Aided Engineering），即计算机辅助工程，是利用计算机技术进行工程设计、分析和优化的重要手段。随着CAE技术的不断发展，其应用范围越来越广泛，用户群体也越来越庞大。为了更好地了解和服务用户，将CAE用户划分为以下几类：

第一类用户：CAE小白

这类用户对CAE技术了解甚少，甚至不清楚CAE的作用。他们往往将CAE软件视为万能工具，希望直接得到最优解。例如：

  • 我有一个CAD模型，CAE分析软件就应该给我得到一个最优解。
  • 我CAD已经设计好了，你的CAE软件要找出我设计中的问题，并优化我的结构，最终给我一个最优的结构设计。

这类用户的特点是：

  • 不清楚CAE的作用
  • 不清楚自己的问题
  • 对CAE软件的功能和局限性认识不足

第二类用户：经验丰富但缺乏CAE专业知识

这类用户在工程实践中积累了丰富的经验，对产品的性能和质量有深刻的理解。他们往往遇到一些产品在生产过程中总是出现同样的问题，对于产生这个问题的原因有自己的认识，但缺乏CAE专业知识，无法有效解决问题。例如：

  • 产品在使用过程中经常出现断裂，我怀疑是材料问题，但不知道如何验证。
  • 产品的散热效果不佳，我需要改进散热设计，但不知道如何下手。

这类用户的特点是：

  • 了解自己的问题
  • 不了解CAE软件的限制以及细分
  • 希望借助CAE技术解决实际问题

第三类用户：CAE专业人士

这类用户是CAE领域的专业人士，他们对CAE技术有深入的了解，熟悉CAE软件的功能和应用范围。他们往往需要针对特定的问题选择合适的CAE软件进行分析和优化。例如：

  • 我需要进行流体分析，请问哪款CAE软件比较适合？
  • 我需要进行结构分析，请问如何使用CAE软件进行仿真？

这类用户的特点是：

  • 了解自己的问题
  • 了解CAE软件的限制以及细分
  • 能够熟练使用CAE软件进行分析和优化

如何更好地服务CAE用户

针对不同类型的CAE用户，需要提供不同的服务策略：

  • 对于第一类用户，需要加强CAE基础知识的普及，帮助他们了解CAE的作用和应用范围。同时，要提供一些简单易用的CAE工具，降低用户的使用门槛。
  • 对于第二类用户，需要提供针对性强的CAE技术咨询服务，帮助他们解决实际问题。同时，可以举办一些CAE技术培训课程，帮助他们提升CAE专业知识。
  • 对于第三类用户，需要提供专业的CAE技术支持服务，帮助他们选择合适的CAE软件，并解决使用过程中的问题。同时，可以建立CAE技术交流平台，促进用户之间的经验分享。

总之，要更好地服务CAE用户，需要对不同类型的用户进行精准分析，并提供差异化的服务策略。只有这样，才能充分满足用户需求，促进CAE技术的推广应用。

初识有限元分析误差

有限元分析（Finite Element Analysis，简称FEA）是一种广泛应用于工程和科学领域的数值方法，用于求解复杂物理系统的近似解。尽管有限元方法在求解偏微分方程和结构分析等方面表现出色，但它本质上仍是一种近似方法。因此，理解和控制有限元分析过程中的各种误差，对于确保计算结果的准确性和可靠性至关重要。本文将从建模误差、用户误差、离散化误差、截断误差和舍入误差、操作误差等方面探讨有限元分析中的误差来源，并介绍有限元计算误差的测试和估计方法及其应用。

建模误差

建模误差是指在将物理过程转换为数学模型时所产生的误差。物理现象通常复杂多变，然而为了使问题能够在有限元框架下解决，必须对其进行简化和假设。例如，在进行结构分析时，可能会假设材料均匀、各向同性，或忽略某些边界条件和外部因素。这些简化和假设虽然能大大降低计算复杂度，但也可能导致模型与实际物理过程之间产生差异，从而引入建模误差。

应对建模误差的策略包括：

  • 改进模型的精确度：通过更细致的物理建模和考虑更多的影响因素来减少误差。
  • 多模型对比：使用不同的数学模型对同一物理问题进行分析，比较结果以评估建模误差的影响。

用户误差

用户误差是指用户在分析物理问题、进行有限元建模和求解过程中由于知识水平、经验不足或操作失误所导致的误差。用户误差主要包括以下几个方面：

  • 问题定义错误：用户对物理问题的理解不准确，导致错误的模型定义。
  • 参数设置错误：材料属性、边界条件、载荷条件等参数设置不当。
  • 网格划分不合理：网格划分过粗或过细，导致计算结果不准确或计算量过大。

减少用户误差的关键在于提高用户的专业知识水平和操作技能，并加强对有限元分析软件的培训。同时，借助自动化工具和智能化技术，如自动网格划分、参数优化等，可以有效降低用户误差。

离散化误差

离散化误差是有限元分析中的一种主要误差来源。有限元方法通过将连续的求解域离散化为有限多个单元，并在这些单元上进行近似求解。离散化过程不可避免地会引入误差，主要表现为：

  • 网格密度：网格越密，离散化误差越小，但计算量也会显著增加。
  • 单元类型和形状：不同类型和形状的单元在逼近能力和计算效率上存在差异。
  • 插值函数选择：高阶插值函数可以提供更高的精度，但计算复杂度也相应增加。

为了控制离散化误差，可以采取以下措施：

  • 合理网格划分：在关键区域采用较密的网格，在非关键区域采用较稀的网格。
  • 优化单元类型和形状：根据问题特点选择合适的单元类型和形状。
  • 使用高阶插值函数：在计算资源允许的情况下，使用高阶插值函数以提高计算精度。

截断误差和舍入误差

截断误差和舍入误差是数值计算中常见的误差类型。截断误差是由于数值方法本身的有限性而引入的误差。例如，数值积分和数值微分方法通常只能给出近似解，其精度取决于步长和方法的阶数。舍入误差则是由于计算机在进行浮点运算时，无法精确表示所有实数而引入的误差。

在有限元分析中，控制截断误差和舍入误差的方法包括：

  • 选择高精度数值方法：例如，使用高阶数值积分和微分方法。
  • 优化算法和程序：减少不必要的运算次数，降低舍入误差的累积效应。
  • 使用高精度浮点数：在关键计算中使用双精度或多精度浮点数。

操作误差

操作误差是指在有限元分析过程中，由于数值计算结果传递过程中产生的误差。这种误差通常在多步计算和复杂系统的分析中尤为明显。例如，在结构动力学分析中，时间步进法的选择和稳定性直接影响计算结果的精度。

为了减少操作误差，可以采取以下措施：

  • 选择稳定的数值算法：确保数值方法在整个计算过程中的稳定性。
  • 精细化时间步长：在动态分析中，选择合适的时间步长以平衡计算精度和效率。
  • 结果验证和修正：在关键步骤进行结果验证，并根据需要进行修正。

有限元计算过程误差测试方法

为了确保有限元分析结果的可靠性，必须对计算过程中的误差进行测试和评估。常用的误差测试方法包括：

  • 收敛性测试：通过逐步细化网格或时间步长，观察计算结果的收敛性，以评估离散化误差。
  • 误差估计技术：利用后验误差估计方法，对计算结果的误差进行评估和控制，如残差法、能量法等。
  • 对比实验：将有限元分析结果与实验结果或解析解进行对比，评估模型和计算方法的准确性。

有限元计算的误差估计方法

误差估计是提高有限元分析结果精度的重要手段。常用的误差估计方法包括：

  • 残差法：通过计算数值解与精确解（或近似精确解）的残差，评估误差大小。
  • 能量法：基于能量范数，评估数值解与精确解之间的能量差异。
  • 自适应方法：根据误差估计结果，自动调整网格密度或时间步长，以提高计算精度。

这些误差估计方法在工程实践中有广泛应用。例如，在结构分析中，通过误差估计可以识别和加强关键区域的网格划分，从而提高整体计算精度。在流体动力学分析中，自适应网格技术能有效捕捉流场中的细节特征，显著提升计算效果。

应用实例

为了更好地理解有限元分析中的误差控制，我们可以通过具体的应用实例进行说明。例如，在桥梁结构的有限元分析中：

  • 建模误差：通过精确测量桥梁材料属性和外部载荷条件，减少建模误差。
  • 用户误差：使用经验丰富的工程师进行模型建立和参数设置，同时借助自动化工具辅助操作。
  • 离散化误差：在应力集中区域采用更密的网格划分，并选择合适的单元类型。
  • 截断误差和舍入误差：使用高精度数值积分方法，并在关键计算中采用双精度浮点数。
  • 操作误差：选择稳定的时间步进法，优化计算流程。

通过以上措施，能够有效控制有限元分析中的各类误差，确保计算结果的准确性和可靠性。

结论

有限元分析作为一种强大的数值方法，广泛应用于工程和科学领域。然而，有限元方法本质上是一种近似解法，理解和控制误差是保证计算结果准确性和可靠性的关键。通过系统分析建模误差、用户误差、离散化误差、截断误差和舍入误差、操作误差等来源，并采取相应的测试和估计方法，可以显著提高有限元分析的精度和可靠性。在实际应用中，工程师应结合具体问题特点，灵活运用各种误差控制手段，确保有限元分析结果的科学性和实用性。

有限元分析简介

有限元分析（Finite Element Analysis，FEA）是一种数值方法，用于求解复杂物理现象的近似解。通过将复杂的连续体分割成有限个小单元，应用物理学定律求解每个单元的响应，然后组合这些响应以获得整体问题的解。本文将从有限元分析的基本思想、解析解和近似解、有限元问题的分类、有限元建模、有限元离散化、有限元分析的误差来源以及通用有限元软件的一般分析步骤七个方面进行详细阐述。

1. 有限元分析基本思想

有限元分析的基本思想是将复杂的物理问题离散化，分解成许多小的、简单的单元（finite elements），并通过建立单元的方程，利用数值方法进行求解。具体而言，将研究对象划分为有限个单元（如三角形、四边形、立方体等），在每个单元内部假设一个简单的近似函数（通常是多项式），然后将这些单元的方程通过边界条件和相邻单元的相互关系组合起来，从而形成整个问题的方程组。通过求解这些方程组，可以得到整个系统的近似解。

2. 解析解和近似解

解析解（analytical solution）是指通过数学解析方法得出的精确解，它通常适用于简单的几何形状和边界条件。然而，许多实际工程问题的几何形状复杂、边界条件多变，使得求解析解变得极其困难甚至不可能。因此，近似解（approximate solution）成为求解复杂工程问题的主要方法。有限元分析便是一种重要的数值近似方法，通过离散化和数值计算，提供工程问题的近似解，虽然不能精确求解，但在工程应用中足够精确和有效。

3. 有限元问题的分类

有限元问题主要分为结构分析、热传导分析、流体动力学分析、电磁场分析等几类。

  • 结构分析：研究结构在载荷作用下的变形、应力和应变分布，常用于桥梁、建筑和机械部件等工程领域。
  • 热传导分析：研究物体的温度分布及其随时间的变化，应用于电子设备散热、热力设备设计等。
  • 流体动力学分析：研究流体的流动特性，包括速度场、压力场和湍流等，广泛应用于航空航天、汽车工程和环境科学等。
  • 电磁场分析：研究电磁场的分布及其对物质的作用，应用于电机设计、电磁兼容和通信工程等领域。

4. 有限元建模

有限元建模是将物理问题转化为有限元形式的过程。首先，需要对实际问题进行简化和抽象，建立数学模型。然后，选择合适的有限元类型和单元形状，对模型进行离散化，划分网格。接下来，确定每个单元的节点及其连接关系，设定材料属性和边界条件。最后，生成有限元模型，准备进行数值求解。有限元建模的质量直接影响分析结果的准确性和计算效率。

5. 有限元离散化

有限元离散化是将连续体分割成有限个小单元的过程。离散化的步骤包括选择合适的单元类型（如线性单元、二次单元等）、划分网格、确定节点位置和单元连接关系。离散化的目标是用有限个单元和节点来逼近原问题的几何形状和物理特性。网格划分的细密程度和单元类型的选择会影响计算结果的精度和计算量。通常，网格划分越细密，计算结果越精确，但计算量也越大。

6. 有限元分析的误差来源

有限元分析的误差主要来源于以下几个方面：

  • 模型简化误差：由于实际工程问题的复杂性，建立有限元模型时通常需要进行简化和假设，这可能导致一定的误差。
  • 离散化误差：由于将连续体离散化为有限个单元，无法完全精确描述原问题，导致离散化误差。网格划分的精细程度直接影响离散化误差的大小。
  • 数值计算误差：在求解有限元方程组时，由于数值方法的近似性和计算机运算精度的限制，会产生数值计算误差。
  • 输入参数误差：材料属性、边界条件等输入参数的测量误差或不准确性也会引入误差。

7. 通用有限元软件一般分析步骤

使用通用有限元软件进行分析通常包括以下几个步骤：

  1. 前处理：
  • 建立几何模型：根据实际工程问题，建立对应的几何模型。
  • 网格划分：选择合适的单元类型和划分策略，对几何模型进行离散化。
  • 定义材料属性和边界条件：设定材料的力学性能参数，施加外力、位移和其他边界条件。
  1. 求解：
  • 建立有限元方程组：根据离散化后的模型，生成对应的有限元方程组。
  • 选择求解方法：选择适当的数值求解算法，如直接法或迭代法，进行方程组求解。
  1. 后处理：
  • 结果可视化：将求解得到的结果（如位移、应力、温度场等）进行图形化显示，便于分析和理解。
  • 结果分析：根据可视化结果，进行工程分析和评估，判断结构的安全性和可靠性。
  1. 模型验证与优化：
  • 验证模型：通过实验数据或其他数值方法验证有限元模型的准确性。
  • 模型优化：根据分析结果，对有限元模型进行优化和改进，提高分析精度和效率。

总结

有限元分析作为一种强大的数值计算工具，在工程实践中得到了广泛应用。通过有限元分析，可以有效解决复杂结构、热传导、流体动力学和电磁场等问题，提供工程设计和分析的重要依据。尽管有限元分析存在一定的误差和局限性，但随着计算机技术和数值算法的发展，其精度和效率不断提高，为科学研究和工程应用提供了更加可靠和便捷的手段。通过深入理解有限元分析的基本原理和方法，并结合实际工程问题进行合理建模和求解，可以充分发挥其在工程领域的巨大潜力和优势。

焊接有限元仿真简介

焊接是将两块或多块金属材料通过加热或加压或两者都用，实现材料永久连接在一起的一种工艺方法。它广泛应用于航空航天、造船、汽车、工程机械行业等各个领域。

焊接有限元仿真是一种利用有限元分析（FEA）技术来模拟焊接过程的计算机技术。它可以用于预测焊接过程中的温度分布、残余应力、变形等，从而帮助工程师设计更安全、更可靠的焊接结构。

焊接工艺的特点

焊接工艺的特点主要体现在以下几个方面：

  • 非线性: 焊接过程是一个非线性热力学耦合过程，涉及热传递、塑性变形、相变等多种物理现象。
  • 局部的: 焊接热源会引起材料在局部区域的剧烈变化，导致材料性能发生变化。
  • 动态的: 焊接过程是一个动态过程，随着时间的推移，温度、应力、变形等都会发生变化。

焊接工艺方法

焊接工艺方法主要包括以下几种：

  • 熔化焊接: 利用热源（如电弧、激光、电子束等）使金属材料熔化，并形成熔池。然后，填充金属（焊条、焊丝等）在熔池中凝固，形成焊缝。
  • 压力焊接: 不使用外部热源，而采用压力使金属材料塑性变形并连接在一起。压力焊接方法主要包括锻焊、挤压焊、摩擦焊等。
  • 化学焊接: 利用化学反应使金属材料连接在一起。化学焊接方法主要包括钎焊、粘接等。

SYSWELD焊接仿真软件

SYSWELD是一款功能强大的焊接仿真软件，可以用于模拟各种焊接工艺过程。它具有以下特点：

  • 支持多种焊接工艺: SYSWELD支持熔化焊接、压力焊接和搅拌摩擦焊等多种焊接工艺。
  • 可以模拟复杂的焊接过程: SYSWELD可以模拟三维焊接过程，并考虑材料的非线性行为、局部效应和动态效应。
  • 提供丰富的分析结果: SYSWELD可以提供温度分布、残余应力、变形等多种分析结果。

SYSWELD可以帮助工程师设计更安全、更可靠的焊接结构，并减少焊接缺陷的产生。

以下是一些SYSWELD的应用案例：

  • 预测焊接变形: SYSWELD可以用于预测焊接过程中的变形，从而帮助工程师设计更合理的焊接夹具和工装。
  • 评估焊接残余应力: SYSWELD可以用于评估焊接残余应力，从而帮助工程师选择合适的焊接工艺和材料。
  • 分析焊接缺陷: SYSWELD可以用于分析焊接缺陷的形成机理，从而帮助工程师改进焊接工艺。

总结

焊接有限元仿真技术可以帮助工程师设计更安全、更可靠的焊接结构，并减少焊接缺陷的产生。SYSWELD是一款功能强大的焊接仿真软件，可以用于模拟各种焊接工艺过程，并提供丰富的分析结果。

欢迎各位交流关于焊接仿真的问题（WeChat)

培养孩子的自我激励：从外在奖励到内在动力的转变

在孩子的成长过程中，家长和教育者都希望能够激发孩子的学习兴趣和积极性，让他们拥有内在的动力，主动地学习和探索。传统的教育方式通常采用通过外在奖励来提高孩子的积极性，例如通过物质奖励来鼓励孩子完成任务或者学习新知识。然而，随着人们对教育的认识和理解的不断深入，越来越多的人开始意识到，这种通过外在奖励来提高孩子积极性的方式存在一定的局限性，甚至可能会产生负面的影响。因此，越来越多的家长和教育者开始关注如何培养孩子的自我激励，让孩子拥有内在的动力和动机。

外在激励法是通过外部奖励来提高孩子的积极性，例如奖励他们的好成绩或者完成任务的好表现。这种方法能够立即激发孩子的积极性，让他们更容易达到目标。而内在激励法则是通过让孩子自我激励来提高孩子的积极性，例如让孩子自己设定目标并且找到实现目标的方法。这种方法需要孩子在内心寻找到真正的动力和动机，可以培养孩子的自我控制和解决问题的能力。

外在激励法可能会让孩子对外部奖励过于依赖，减少他们的自我激励和自我控制能力。如果孩子在获得奖励之后遇到困难或者面临挑战，他们可能会变得失望和无助，缺乏继续努力的动力。

内在激励法可以让孩子建立起自我激励的能力，拥有内在的动机和积极性。这种方法可以让孩子自己设定目标和寻找实现目标的方法，培养他们的自我控制和解决问题的能力。在孩子面临挑战或者困难时，他们可以从内心中寻找动力和勇气，继续坚持下去。

据研究，70%的美国父母倾向于使用外部奖励来激励孩子的学习和行为表现。这种做法在某些情况下确实可以激发孩子的积极性和动力，但是如果长期使用，会让孩子过度依赖外部奖励，减少他们的自我激励能力。

然而，随着社会的进步和家长对教育的更深入思考，越来越多的家长开始意识到使用外在奖励的教育方法的局限性和问题，并开始寻找更加科学和有效的教育方法。

培养孩子的自我激励是一个需要时间和过程的转变，需要家长和教育者有耐心和信心。以下是一些建议，帮助家长和教育者引导孩子从外在奖励到内在动力的转变：

  1. 逐渐减少外在奖励。家长可以从小减少孩子接受的物质奖励，例如糖果或小礼物等，鼓励孩子学会从内在动机中获得快乐和成就感。家长可以和孩子一起讨论，让孩子明白完成任务和学习新知识的意义和价值，从而让他们慢慢地开始寻求内在的满足感。
  2. 帮助孩子制定自我激励的目标。在孩子完成某个任务或者学习新技能时，家长可以和孩子一起制定目标，并且鼓励他们为实现目标而努力。目标可以是小的、可达成的目标，例如写完一篇作文或者掌握一项新技能等，让孩子感受到实现目标的满足感和成就感。
  3. 给予孩子肯定和支持。当孩子努力实现目标时，家长要及时给予肯定和支持，让孩子感受到自己的努力是有价值的，从而增强他们的自信心。家长可以对孩子的进步和成就进行肯定
  4. 让孩子意识到自己的努力是被认可和重视的，这样可以激发他们更多的积极性和自我激励。
  5. 培养孩子的自我控制能力。自我控制是培养自我激励的重要能力之一。家长可以通过游戏和其他活动来帮助孩子培养自我控制能力，例如要求孩子在玩具堆里选择一件玩具，或者在看电视时限制孩子的时间。在这个过程中，家长可以引导孩子思考和解决问题的方法，让他们自己想出最佳的解决方案，从而增强他们的自我控制能力。
  6. 鼓励孩子自我反思。在孩子完成任务或者学习新知识后，家长可以和孩子一起回顾学习过程，让孩子自我反思自己的表现和取得的成就。在这个过程中，家长可以帮助孩子找到自己的优点和不足，并且鼓励他们进一步改进自己的表现。

教育孩子是一项长期而艰巨的任务，需要家长们不断地学习和进步。外在奖励的教育方法在一定程度上可以激发孩子的积极性和兴趣，但其局限性和问题也越来越明显。采用内在动力的教育方法可以更加有效地培养孩子的自我激励能力，让他们在学习和生活中取得更好的成绩和体验。家长们可以通过一些实践和经验的积累，帮助孩子在内在动力的驱动。除了家长的引导和激励，学校和教师也扮演着重要的角色。学校可以设计一些有趣且富有挑战性的学习任务，让学生感到有成就感和自豪感，从而促进他们的自我激励。教师可以提供鼓励和支持，同时还要注意避免使用过多的外部奖励。此外，教师还可以引导学生制定目标和计划，帮助他们更好地实现自我激励。

总之，培养孩子的自我激励是一个需要家长和教育者慢慢引导和培养的过程。家长需要逐渐减少外在奖励，让孩子从内在动机中寻找快乐和成就感；同时，家长也需要鼓励孩子制定自我激励的目标，给予肯定和支持，培养孩子的自我控制能力，以及鼓励孩子自我反思。通过这些方式，家长和教育者可以帮助孩子逐渐从外在奖励到内在动力的转变，让孩子拥有内在的动机和积极性，更好地适应未来的学习和生活。

探究热塑性材料的制造与应用

  1. 热塑性材料定义

一种可以在一定温度范围内加热软化，冷却后可保持新形态的材料。在热塑性材料中，热塑性复合材料是一种常见的材料类型，它是将树脂和增强材料（如碳纤维、玻璃纤维等）混合而成的复合材料。热塑性复合材料具有较好的强度、刚度、耐热性和耐化学腐蚀性，因此在航空、汽车、体育器材等领域得到广泛应用。

  1. 热塑性材料的主要特点

其分子链可以通过加热软化，并在冷却后重新固化形成新的形态。与热固性材料相比，热塑性材料具有较好的可加工性和可回收性，可以通过注塑、挤出、压缩成型等加工方式制造出各种形状和尺寸的产品。

  1. 可塑性好：热塑性复合材料在加热后可以被塑性变形，易于成型，并可通过热成型等工艺得到不同形状和尺寸的产品。
  2. 可回收性：热塑性复合材料在加热后能够被重新加工、回收，可循环使用，有利于环保。
  3. 耐高温性能好：热塑性复合材料具有较好的高温稳定性能，能够在高温环境下使用。
  4. 耐腐蚀性好：热塑性复合材料具有良好的耐腐蚀性能，适用于一些有腐蚀性的工作环境。
  5. 可定制性强：热塑性复合材料可以根据不同的需求和应用场合进行定制，可制成各种复杂的形状。

热塑性材料的应用领域

  1. 航空航天：热塑性复合材料可以用于制造飞机、航天器等结构件，具有轻质、高强度、抗腐蚀等优点。
  2. 汽车工业：热塑性复合材料可以用于汽车外壳、车门等部件，能够减轻车身重量、提高燃油效率。
  3. 电子电器：热塑性复合材料可以用于制造电子元器件外壳、散热器等部件。
  4. 医疗器械：热塑性复合材料可以用于制造医疗器械外壳、手术器械等部件，具有耐高温、耐腐蚀、可定制等优点。

热塑性复合材料常见产品

  1. 碳纤维增强热塑性复合材料（CFRTP）：由碳纤维和热塑性树脂组成，具有轻质、高强度、高刚度等优点，常用于制造航空航天、汽车、体育器材等产品。
  2. 玻璃纤维增强热塑性复合材料（GFRTP）：由玻璃纤维和热塑性树脂组成，具有较好的耐腐蚀性和绝缘性，常用于制造化工设备、污水处理设备、储罐等产品。
  3. 聚酰亚胺热塑性复合材料（PAI）：由聚酰亚胺和热塑性树脂组成，具有较好的高温性能和耐腐蚀性，常用于制造航空航天、电子电器等产品。
  4. 聚丙烯热塑性复合材料（PP）：由聚丙烯和热塑性树脂组成，具有较好的耐腐蚀性和可塑性，常用于制造家电、汽车零部件等产品。

在热塑性复合材料的生产过程中，常用的工艺包括：

  1. 注塑成型：将热塑性树脂加热到熔化状态，注入模具中，经冷却后得到成型产品。
  2. 压缩成型：将热塑性复合材料层压在一起，加热、加压，使其熔融在一起，冷却后得到成型产品。
  3. 热成型：将热塑性复合材料加热至一定温度，通过各种成型方法（如真空吸塑、热压成型等），使其成型后冷却得到成型产品。

碳纤维增强热塑性复合材料（CFRTP）介绍

热塑性复合材料的一种，其特点是具有较高的强度、刚度和轻量化等优点，广泛应用于航空、汽车、体育器材等领域。CFRTP的制备工艺主要包括材料准备、布料成型、热固化、冷却和后处理等步骤。其中，热成型工艺是将预浸料在高温高压下成型的过程，具体步骤包括将预浸料叠压在模具中，加热压缩，热固化，冷却和后处理等步骤。

碳纤维增强热塑性复合材料（CFRTP）热成型工艺是将热塑性树脂与碳纤维预浸料在高温高压下成型的过程，该工艺可以制造各种形状和尺寸的复合材料产品，包括飞机部件、汽车零件、体育器材、建筑材料等。

下面是碳纤维增强热塑性复合材料热成型工艺的详细步骤：

  1. 材料准备：将碳纤维预浸料与热塑性树脂按照一定比例混合，并在真空下振实，使其充分浸润。
  2. 布料成型：将混合好的预浸料叠压在模具中，经过加热和压缩，使其形成所需的形状。
  3. 热固化：将成型后的布料放入热压机中，加热至一定温度（通常在200℃-400℃之间），并施加高压（通常在20MPa-100MPa之间），使树脂熔化并浸润碳纤维，使其结合成为一体。
  4. 冷却：将热固化后的成品从热压机中取出，放入冷却模具中进行自然冷却或者通过水冷却等方式使其冷却至室温。
  5. 后处理：经过冷却后，可根据需要进行切割、打磨等后处理操作，最终得到所需的碳纤维增强热塑性复合材料产品。

总的来说，热塑性材料具有可加工性好、可回收性强、可调性等优点，广泛应用于各个领域。而CFRTP则是热塑性复合材料的一种，具有轻量化、高强度、高刚度等优点，其制备工艺主要包括材料准备、布料成型、热固化、冷却和后处理等步骤，是一种重要的高性能复合材料。

CentOS有效的管alias清单

在 CentOS 中，别名的配置保存在 shell 配置文件中。默认情况下，Bash shell 使用 ~/.bashrc 配置文件来定义别名、环境变量和其他 shell 选项。因此，当您定义一个新别名时，它会被保存在 ~/.bashrc 文件中。

如果您想保存您当前 shell 中的别名清单，可以使用以下命令将其输出到文件中：

alias > alias_list.txt

这个命令将别名列表写入一个名为 alias_list.txt 的文件中。您可以将输出文件重命名为其他名称，具体取决于您的喜好和需要。

如果您希望在以后的会话中加载别名列表，请执行以下操作：

  1. 打开一个新的终端。
  2. 进入您的 home 目录。在命令行中输入以下命令并按回车键：
cd ~

使用文本编辑器打开 ~/.bashrc 文件。在命令行中输入以下命令并按回车键：

vi .bashrc

将以下命令添加到文件末尾：

bash
# 加载别名列表
if [ -f ~/alias_list.txt ]; then
    . ~/alias_list.txt
fi

这个命令会检查您的 home 目录下是否存在 alias_list.txt 文件，如果存在，则会将其读取到当前 shell 中。

保存并关闭文件。在命令行中输入以下命令并按回车键：

:wq

使更改生效。在命令行中输入以下命令并按回车键：

source .bashrc

现在，每当您打开一个新终端时，都会自动加载您之前保存的别名列表。

Ubuntu20.04安装RDP远程桌面

Ubuntu安装远程桌面非常容易设置。它只需要几个简单的步骤。

这个篇文章讲的是使用 RDP客户端连接您的远程 VPS。

以下命令适合UBUNTU20.04,VPS是AWS.

  1. 创建服务器和SSH连接

首先，您需要在 AWS 上创建一个 Ubuntu 20.04 的 VPS 实例。一旦创建成功，您可以通过 SSH 连接到 VPS。在终端中输入以下命令：

ssh your_username@your_server_ip_address

将 “your_username” 替换为您的用户名，”your_server_ip_address” 替换为您 VPS 的公共 IP 地址。如果是第一次连接 VPS，则需要进行身份验证。

同样的你也可以用第三方的工具连接VPS。

  1. 添加新的管理员用户

在连接到 VPS 后，您需要创建一个新的管理员用户。我们将在此用户下安装 GUI 和配置 RDP 服务器。

arduino
sudo -i
adduser rdpuser  # rdpuser 为新添加的用户名

然后设置新用户的密码：

passwd rdpuser

接下来，您需要将新用户添加到 sudo 组中，以便他拥有管理权限。

sudo usermod -a -G sudo rdpuser
  1. 安装 Ubuntu 图形用户界面 (GUI)

现在您需要在 VPS 上安装 Ubuntu 的图形用户界面。

sql
sudo apt update
sudo apt install ubuntu-desktop

这会下载和安装大量的软件包，因此可能需要一些时间。

  1. 安装和配置 RDP 服务器

接下来，您需要安装和配置 RDP 服务器。在终端中输入以下命令：

sudo apt install xrdp
sudo systemctl status xrdp
sudo vim /etc/xrdp/xrdp.ini

第一行将安装 xrdp，第二行将检查 xrdp 服务器的状态。如果服务已经运行，则会显示“active (running)”消息。第三行将打开 xrdp.ini 文件进行编辑。

找到并编辑以下行：

port=tcp://:3389

确保端口号是 3389。保存并关闭文件。接下来，您需要重启 xrdp 服务器。

sudo systemctl restart xrdp
  1. AWS 后台打开 3389 端口

在 AWS 控制台中打开 3389 端口。在 “安全组” 设置中添加一个新的入站规则，类型选择为 “RDP”，来源选择为 “0.0.0.0/0″。

  1. 在 VPS 中也要打开 3389 端口

如果您的 VPS 启用了防火墙，您还需要在 VPS 中打开 3389 端口。在终端中输入以下命令：

yaml
sudo ufw allow 3389

好了，现在您可以使用 RDP 客户端连接到您的 Ubuntu 20.04 VPS，享受桌面体验了！

如何在Arm架构上的VPS安装Hestiacp

今天能够撸到Oracle Cloud 的Arm服务器也是不容易的。

要安装此控制面板需要的准备工作：

  1. 甲骨谷文Arm架构的服务器一台；
  2. Ubuntu20.04系统

此文单主要介绍如何安装，主要有如下步骤：

  1. 使用SSH工具连接VPS，并进入root用户。命令：sudo -i
  2. 获取软件。命令：wget https://raw.githubusercontent.com/hestiacp/hestiacp/release/install/hst-install.sh
  3. 安装软件。命令：bash hst-install.sh；如果不能安装，执行后面的命令：bash hst-install.sh -f
  4. 完成后将相关信息保存下来。
  5. 你可以用你的ip+port(安装完成信息的提示）。